Have you ever wondered how the movie recommendations on Netflix are made? I am always fascinated by how their recommendations are made, and they seem to know my preference better than my self. Such recommendation systems are very complex, but mostly base on a technique called collaborative filtering. This basically means to look at the current user ‘s previous ratings, find other users with the same preferences, and recommend the current user the products that have been positively rated by the similar users.
In this post, we will employ the Movielens dataset to train a recommender system with collaborative filtering. This dataset contains 100000 ratings from 943 users on 1682 movies, where each user has rated at least 20 movies. Although the dataset also contains further interesting information that might be helpful, we will only concentrate on the correlation of user ratings.
Prepare the dataset
import pandas as pd
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader
import torch.utils.data as data_utils
import numpy as np
import math
from sklearn.model_selection import train_test_split
import copy
import matplotlib.pyplot as plt
import torch.utils.data as data_utils
from sklearn.decomposition import PCA
# load the rating data
path = "/content/ml-100k/"
ratings = pd.read_csv(path + 'u.data', delimiter='\t', header=None,
usecols=(0,1,2), names=['user','movie','rating'])
ratings.head()
| user | movie | rating | |
|---|---|---|---|
| 0 | 196 | 242 | 3 |
| 1 | 186 | 302 | 3 |
| 2 | 22 | 377 | 1 |
| 3 | 244 | 51 | 2 |
| 4 | 166 | 346 | 1 |
# load the movie data
movies = pd.read_csv(path + 'u.item', delimiter='|', encoding='latin-1',
usecols=(0,1), names=('movie','title'), header=None)
movies.head()
| movie | title | |
|---|---|---|
| 0 | 1 | Toy Story (1995) |
| 1 | 2 | GoldenEye (1995) |
| 2 | 3 | Four Rooms (1995) |
| 3 | 4 | Get Shorty (1995) |
| 4 | 5 | Copycat (1995) |
# merge the dataset
ratings = ratings.merge(movies)
ratings.head()
| user | movie | rating | title | |
|---|---|---|---|---|
| 0 | 196 | 242 | 3 | Kolya (1996) |
| 1 | 63 | 242 | 3 | Kolya (1996) |
| 2 | 226 | 242 | 5 | Kolya (1996) |
| 3 | 154 | 242 | 3 | Kolya (1996) |
| 4 | 306 | 242 | 5 | Kolya (1996) |
ratings['user'] = ratings['user'] -1
ratings['movie'] = ratings['movie'] -1
movies['movie'] = movies['movie'] -1
dataset_sizes = ratings.shape
dataset_sizes
(100000, 4)
n_users = len(ratings["user"].unique())
n_movies = len(ratings["movie"].unique())
n_users, n_movies
(943, 1682)
# movies with max. number of ratings
ratings["title"].value_counts()[:20]
Star Wars (1977) 583
Contact (1997) 509
Fargo (1996) 508
Return of the Jedi (1983) 507
Liar Liar (1997) 485
English Patient, The (1996) 481
Scream (1996) 478
Toy Story (1995) 452
Air Force One (1997) 431
Independence Day (ID4) (1996) 429
Raiders of the Lost Ark (1981) 420
Godfather, The (1972) 413
Pulp Fiction (1994) 394
Twelve Monkeys (1995) 392
Silence of the Lambs, The (1991) 390
Jerry Maguire (1996) 384
Chasing Amy (1997) 379
Rock, The (1996) 378
Empire Strikes Back, The (1980) 367
Star Trek: First Contact (1996) 365
Name: title, dtype: int64
device = 'cuda:0' if torch.cuda.is_available() else 'cpu'
target = torch.tensor(ratings['rating'].values.astype(np.float32), device=device)[..., np.newaxis]
features = torch.tensor(ratings.drop(['rating', 'title'], axis = 1).values.astype(np.int32), device=device)
# split datasets
data_tensor = data_utils.TensorDataset(features, target)
train_data, test_data = train_test_split(data_tensor, test_size=0.2, random_state=42)
len(train_data), len(test_data)
(80000, 20000)
bs = 100
train_loader = data_utils.DataLoader(train_data, batch_size=bs, shuffle=True)
test_loader = data_utils.DataLoader(test_data, batch_size=bs, shuffle=True)
Define the model
In this section, we are going to use Pytorch to build our network. Our network is made up of 4 embedding layers, which map the user or movie id to some latent spaces that are described in the following. The user_factors embedding layers represent the correlation between each user preferences. The movie_factors layer, on the other hand, describes the correlation between movies. Of course, some movies are inherently good and bad, independent of user ratings, so we need a movie_bias to store this information. Likewise, some users are more critical than the other, and the user_bias encodes this information.
We see that these 4 layers contain exactly the core idea of collaborative filtering. Using deep learning, these layers can be learnt directly from user ratings, just using user id and movie id, regardless of any further information. We will see in the next section that this is enough to make good recommendation.
# helper function to force predictions to be between 0 and 5.
def sigmoid_range(x, low, high):
"Sigmoid function with range `(low, high)`"
return torch.sigmoid(x) * (high - low) + low
Pytorch provieds a very simple way to define an embedding layer, namely with nn.Embedding:
class EmbeddingNet(nn.Module):
def __init__(self, n_users, n_movies, n_factors = 10, y_range=(0,5.5)):
super().__init__()
self.user_factors = nn.Embedding(n_users, n_factors)
self.user_bias = nn.Embedding(n_users, 1)
self.movie_factors = nn.Embedding(n_movies, n_factors)
self.movie_bias = nn.Embedding(n_movies, 1)
self.y_range = y_range
def forward(self, user_idx, movie_idx):
users = self.user_factors(user_idx)
movies = self.movie_factors(movie_idx)
res = (users * movies).sum(dim=1, keepdim=True)
res += self.user_bias(user_idx) + self.movie_bias(movie_idx)
return sigmoid_range(res, *self.y_range)
Define traing objects
# training loop parameters
lr = 3e-3
wd = 3e-4
n_epochs = 30
patience = 20
no_improvements = 0
best_loss = np.inf
best_weights = None
n_factors = 50
model = EmbeddingNet(n_users, n_movies, n_factors).to(device)
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=lr, weight_decay=wd)
scheduler = optim.lr_scheduler.LinearLR(optimizer, start_factor=0.5, total_iters=10)
Show model info:
model
EmbeddingNet(
(user_factors): Embedding(943, 50)
(user_bias): Embedding(943, 1)
(movie_factors): Embedding(1682, 50)
(movie_bias): Embedding(1682, 1)
)
Train the model
train_history = []
val_history = []
lr_history = []
best_loss = 1e3
for i in range(n_epochs):
train_loss = 0
n_batches = 0
# train phase
for features, targets in train_loader:
optimizer.zero_grad()
output = model(features[...,0], features[...,1])
loss = criterion(output, targets)
loss.backward()
optimizer.step()
train_loss += loss.detach()
n_batches += 1
#scheduler.step()
train_loss = train_loss/n_batches
train_history.append(train_loss)
lr_history.append(scheduler.get_last_lr())
# validation
n_batches = 0
val_loss = 0
with torch.no_grad():
for features, targets in test_loader:
output = model(features[...,0], features[...,1])
loss = criterion(output, targets)
val_loss += loss
n_batches += 1
val_loss = val_loss/n_batches
val_history.append(val_loss)
if (val_loss < best_loss):
best_weights = copy.deepcopy(model.state_dict())
best_loss = val_loss
print("Epoch {}, train_loss: {}, val_loss: {}"
.format(i, train_loss.cpu().numpy(), val_loss.cpu().numpy()))
#model.load_state_dict(best_weights)
Epoch 0, train_loss: 7.457712173461914, val_loss: 7.2247538566589355
Epoch 1, train_loss: 6.389175891876221, val_loss: 6.712790012359619
Epoch 2, train_loss: 5.461848258972168, val_loss: 6.160996913909912
Epoch 3, train_loss: 4.655222415924072, val_loss: 5.5575456619262695
Epoch 4, train_loss: 3.8971118927001953, val_loss: 4.903194904327393
Epoch 5, train_loss: 3.1772820949554443, val_loss: 4.215761184692383
Epoch 6, train_loss: 2.510025978088379, val_loss: 3.52919340133667
Epoch 7, train_loss: 1.9204601049423218, val_loss: 2.887474298477173
Epoch 8, train_loss: 1.4384808540344238, val_loss: 2.3278536796569824
Epoch 9, train_loss: 1.0748509168624878, val_loss: 1.8732044696807861
Epoch 10, train_loss: 0.8238030076026917, val_loss: 1.5306777954101562
Epoch 11, train_loss: 0.669340193271637, val_loss: 1.2942407131195068
Epoch 12, train_loss: 0.5864189267158508, val_loss: 1.1392508745193481
Epoch 13, train_loss: 0.5462559461593628, val_loss: 1.041947603225708
Epoch 14, train_loss: 0.5291838049888611, val_loss: 0.9798373579978943
Epoch 15, train_loss: 0.5221965312957764, val_loss: 0.9406192302703857
Epoch 16, train_loss: 0.5192626714706421, val_loss: 0.9124849438667297
Epoch 17, train_loss: 0.5155234932899475, val_loss: 0.8936429023742676
Epoch 18, train_loss: 0.5117744207382202, val_loss: 0.8807430267333984
Epoch 19, train_loss: 0.5071832537651062, val_loss: 0.8699108362197876
Epoch 20, train_loss: 0.5019437074661255, val_loss: 0.8627417087554932
Epoch 21, train_loss: 0.49624019861221313, val_loss: 0.8580852746963501
Epoch 22, train_loss: 0.4914500415325165, val_loss: 0.8545466661453247
Epoch 23, train_loss: 0.4865557551383972, val_loss: 0.8525440692901611
Epoch 24, train_loss: 0.4807068109512329, val_loss: 0.8509074449539185
Epoch 25, train_loss: 0.47658705711364746, val_loss: 0.849090039730072
Epoch 26, train_loss: 0.4731192886829376, val_loss: 0.8473911285400391
Epoch 27, train_loss: 0.46931734681129456, val_loss: 0.8465709090232849
Epoch 28, train_loss: 0.4657156467437744, val_loss: 0.8458096385002136
Epoch 29, train_loss: 0.4617335796356201, val_loss: 0.8460785746574402
model.load_state_dict(best_weights)
<All keys matched successfully>
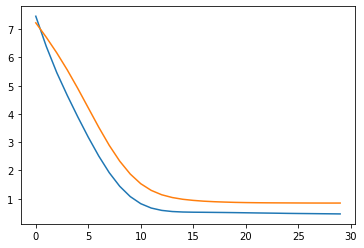
Visualize training history
train_history = np.asarray(train_history)
val_history = np.asarray(val_history)
lr_history = np.asarray(lr_history)
fig = plt.figure()
plt.plot(train_history)
plt.plot(val_history)
[<matplotlib.lines.Line2D at 0x7f81a0f41b10>]
Visualize the Results
def get_movie(ids):
return [movies.loc[id]["title"] for id in ids]
We can try guessing the user ratings on the test set:
with torch.no_grad():
for features, targets in test_loader:
target_predicted = model(features[...,0], features[...,1])
movie_names = get_movie(features[...,1].numpy())
loss = criterion(target_predicted, targets)
print(loss)
target_predicted = target_predicted.squeeze().cpu().numpy()
user_idx = features[...,0].cpu().numpy()
movies_idx = features[...,1].cpu().numpy()
target_real = targets.squeeze().cpu().numpy()
#target_predicted
pred_df = pd.DataFrame(list(zip(user_idx, movies_idx, movie_names, target_real, target_predicted)))
break
pred_df.head(20)
tensor(0.7353)
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 0 | 746 | 418 | Mary Poppins (1964) | 5.0 | 3.960400 |
| 1 | 777 | 404 | Mission: Impossible (1996) | 3.0 | 2.279045 |
| 2 | 785 | 230 | Batman Returns (1992) | 2.0 | 3.065361 |
| 3 | 879 | 139 | Homeward Bound: The Incredible Journey (1993) | 4.0 | 3.125930 |
| 4 | 23 | 257 | Contact (1997) | 4.0 | 4.397166 |
| 5 | 303 | 680 | Wishmaster (1997) | 2.0 | 2.716514 |
| 6 | 59 | 135 | Mr. Smith Goes to Washington (1939) | 4.0 | 4.160026 |
| 7 | 415 | 14 | Mr. Holland's Opus (1995) | 4.0 | 4.215237 |
| 8 | 739 | 331 | Kiss the Girls (1997) | 3.0 | 3.314857 |
| 9 | 886 | 430 | Highlander (1986) | 3.0 | 4.366575 |
| 10 | 933 | 68 | Forrest Gump (1994) | 5.0 | 3.462778 |
| 11 | 84 | 41 | Clerks (1994) | 3.0 | 3.208103 |
| 12 | 881 | 242 | Jungle2Jungle (1997) | 4.0 | 2.592931 |
| 13 | 12 | 910 | Twilight (1998) | 2.0 | 2.822413 |
| 14 | 393 | 402 | Batman (1989) | 4.0 | 3.974622 |
| 15 | 404 | 591 | True Crime (1995) | 1.0 | 1.466990 |
| 16 | 637 | 509 | Magnificent Seven, The (1954) | 3.0 | 3.588601 |
| 17 | 486 | 540 | Mortal Kombat (1995) | 3.0 | 2.984062 |
| 18 | 270 | 413 | My Favorite Year (1982) | 4.0 | 3.552820 |
| 19 | 343 | 123 | Lone Star (1996) | 5.0 | 4.303177 |
We can find out which movies are “the best” and “the worst” just by looking at the movie_bias layer weight:
# lowest
movie_bias = model.movie_bias.weight
idxs = movie_bias.argsort(0)[:5].squeeze().numpy()
get_movie(idxs)
['Children of the Corn: The Gathering (1996)',
'Lawnmower Man 2: Beyond Cyberspace (1996)',
'Mortal Kombat: Annihilation (1997)',
'Jury Duty (1995)',
'Striptease (1996)']
These movies have the IMDB score 4.2, 2.5, 3.7, 4.3, 4.5, respectively. Our model does detect the movies that are not appreciated by film critics.
# highest
idxs = movie_bias.argsort(0, descending=True)[:5].squeeze().numpy()
get_movie(idxs)
["Schindler's List (1993)",
'Shawshank Redemption, The (1994)',
'Casablanca (1942)',
'Rear Window (1954)',
'Star Wars (1977)']
Here also, the model assigns high bias to the movies that actually have very high IMDB scores. This validates the ability of our simple model to find “good” and “bad” movies.
Get top k favourite movies
We can get the k top rated movies as follows:
# get top k movies that have
def get_top_k(k):
with torch.no_grad():
all_bias = model.movie_bias(torch.tensor(np.arange(n_movies), device=device))
idx = all_bias.squeeze().cpu().argsort(descending=True)[:k].squeeze().numpy()
return get_movie(idx), idx
k_name, k_idx = get_top_k(40)
k_name
["Schindler's List (1993)",
'Shawshank Redemption, The (1994)',
'Casablanca (1942)',
'Rear Window (1954)',
'Star Wars (1977)',
'Close Shave, A (1995)',
'Usual Suspects, The (1995)',
'Wrong Trousers, The (1993)',
'Silence of the Lambs, The (1991)',
'Good Will Hunting (1997)',
'Raiders of the Lost Ark (1981)',
'North by Northwest (1959)',
"One Flew Over the Cuckoo's Nest (1975)",
'Vertigo (1958)',
'Titanic (1997)',
'L.A. Confidential (1997)',
'Godfather, The (1972)',
'Boot, Das (1981)',
'To Kill a Mockingbird (1962)',
'12 Angry Men (1957)',
'Wallace & Gromit: The Best of Aardman Animation (1996)',
'Manchurian Candidate, The (1962)',
'As Good As It Gets (1997)',
'Third Man, The (1949)',
'Citizen Kane (1941)',
'Dr. Strangelove or: How I Learned to Stop Worrying and Love the Bomb (1963)',
'Secrets & Lies (1996)',
"It's a Wonderful Life (1946)",
'Empire Strikes Back, The (1980)',
'Fargo (1996)',
'Henry V (1989)',
'Blade Runner (1982)',
'Amadeus (1984)',
'Braveheart (1995)',
'Bridge on the River Kwai, The (1957)',
'Princess Bride, The (1987)',
'Maltese Falcon, The (1941)',
'African Queen, The (1951)',
'Glory (1989)',
'Wizard of Oz, The (1939)']
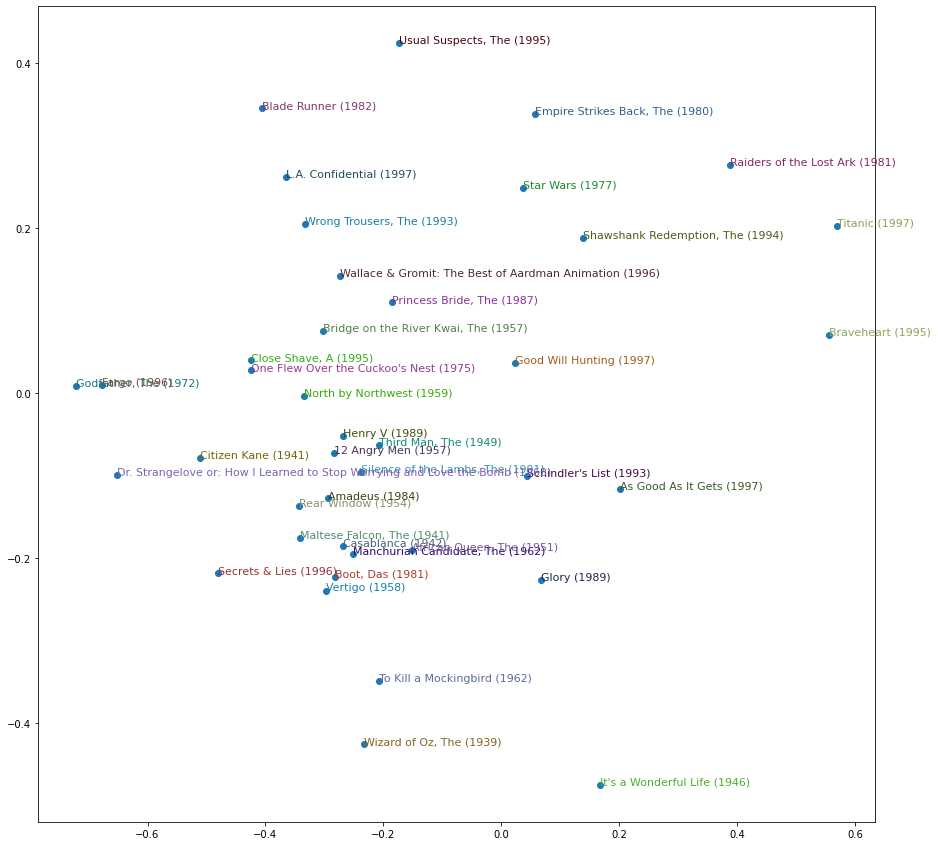
Visualize top k movies
We employed a very large latent space, which is impossible to be visualized. Luckily, we can use the PCA algorithm to reduce the latent space and visualize them:
with torch.no_grad():
movie_factors = model.movie_factors(torch.tensor(np.arange(n_movies), device=device)).cpu().numpy()
pca = PCA(n_components=3)
pca.fit(movie_factors)
reduced_embed = pca.transform(movie_factors)
X = reduced_embed[k_idx][:,0]
Y = reduced_embed[k_idx][:,2]
plt.figure(figsize=(15,15))
plt.scatter(X, Y)
for i, x, y in zip(k_name,X, Y):
plt.text(x,y,i, color=np.random.rand(3)*0.7, fontsize=11)
Make recommendations using distance between 2 movies
To compute the distance betwwem 2 movies, we can compute the cosine distance between their movie_factors (not movie_bias) representation. This allows us to define the similarity in terms of user ratings on both movies.
# helper function
def movie_o2i(s):
return movies[movies["title"] == s]["movie"].values
# get the closest movie
def get_closest_movie(s1):
i1 = torch.tensor(movie_o2i(s1))
movie_factors_torch = torch.tensor(movie_factors)
distances = nn.CosineSimilarity(dim=1)(movie_factors_torch, movie_factors_torch[i1])
idx = distances.argsort(descending=True)[:6].squeeze().numpy()
print(idx)
return get_movie(idx)
s1 = 'Snow White and the Seven Dwarfs (1937)' # kids movie
get_closest_movie(s1)
[ 98 403 500 431 841 135]
['Snow White and the Seven Dwarfs (1937)',
'Pinocchio (1940)',
'Dumbo (1941)',
'Fantasia (1940)',
'Pollyanna (1960)',
'Mr. Smith Goes to Washington (1939)']

We see that our model good a very good recommendation for this example: the recommended movies for “Snow White” are mostly Disney kid movies.
s1 = 'Star Wars (1977)' # the first 2 suggested films are actually star wars film
get_closest_movie(s1)
[ 49 171 180 173 108 122]
['Star Wars (1977)',
'Empire Strikes Back, The (1980)',
'Return of the Jedi (1983)',
'Raiders of the Lost Ark (1981)',
'Mystery Science Theater 3000: The Movie (1996)',
'Frighteners, The (1996)']

Here also, the model recommends very relevant movies for the input movie. Indeed, the first 2 recommendations are also Star wars movie, the next 2 are sci-fi movies, and the last one is a thriller.
Conclusion
In this post, we have trained a simple deep learning model using Pytorch for collaborative filtering. The model is able to identify good and not so good movies, and can make plausible movie recommendations.